Modeling Bivariate Gauge Functions using Bezier Curves
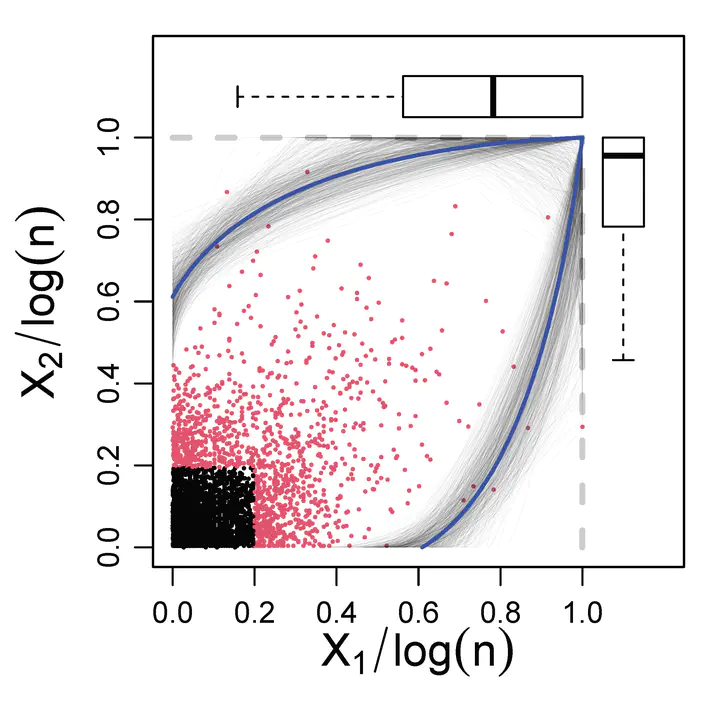 Estimated gauge function for the Santa Ana Winds Data
Estimated gauge function for the Santa Ana Winds DataJoint work with Brian Reich (NCSU), Ben Shaby (CSU), and Dan Cooley (CSU).
A recent trend in (bivariate) extremes analysis focuses on the use of gauge functions which models the entire tail dependence in a geometric manner. Most common measures of tail dependence can also be directly extracted from the form of this gauge function. Current methods usually need to assume a parametric form for the gauge function, which is quite restrictive. We propose the use of Bezier curves which can model complex shapes, and use it in a Bayesian framework to get a full posterior distribution (with uncertainty) of the gauge functions.
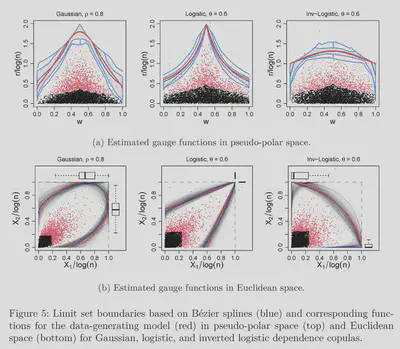
Our approach is flexible, robust, and can identify different regimes of asymptotic behavior that the joint tail exhibits.